La Reducción de Dimensionalidad en el Machine Learning

Normalmente, los algoritmos que se emplean en el Machine Learning son capaces de extraer información importante de conjuntos de datos que cuentan con muchas características, ya sean tablas con muchas columnas y filas o imágenes con millones de píxeles. Si a este hecho se le suman los grandes avances de computación en la nube, el resultado es que cada vez se pueden ejecutar modelos más grandes de aprendizaje automático con una gran potencia.
No obstante, cada característica que se agrega aumenta la complejidad del ejecutable, lo que hace que localizar la información gracias a estos potentes algoritmos también sea complicado. La solución es la reducción de dimensionalidad que consiste en emplear un conjunto de técnicas para eliminar características excesivas y no necesarias de los modelos de Machine Learning.
Asimismo, la reducción de dimensionalidad reduce de forma severa los costes del aprendizaje automático y permite la resolución de problemas complejos con modelos simples.
Esta técnica es especialmente útil en los modelos predictivos, ya que son conjuntos de datos que contienen un elevado número de características de entrada, y hace más complicada su función.
Por tanto, la técnica de reducción de dimensionalidad se define como una forma de convertir un conjunto de datos de dimensiones elevadas en un conjunto de datos de dimensiones menores, asegurando que la información que proporciona en similar en ambos casos. Como se ha mencionado, esta técnica se emplea a menudo en el aprendizaje automático para obtener un modelo predictivo más ajustado mientras se resuelven los problemas de regresión y clasificación que presentan los algoritmos.
Los datos de alta dimensión, el reconocimiento de voz, visualización de datos, reducción de ruido o el procesamiento de señales, entre otros, son los principales campos de aplicación de la reducción de dimensionalidad.
Los problemas de dimensionalidad
Entrando en detalle en los problemas de dimensionalidad que aparecen en los modelos de Machine Learning, primero hay que conocer que estos modelos se encargan de asignar características a resultados. Por ejemplo, un modelo predictivo de climatología cuenta con un conjunto de datos de información recopilada de diferentes fuentes. Estas fuentes incluyen datos de temperatura, humedad, velocidad del viento. Billetes de autobús comprados, tráfico y cantidad de lluvia de diferentes épocas en un mismo lugar. Como se puede observar no todos los datos son relevantes para la predicción del tiempo.
En ocasiones, algunas funciones no estas relacionadas con la variable de destino. Otras características pueden estar correlacionadas con la variable objetivo, pero no tener una relación especifica con ella. También puede haber vínculos entre la característica y la variable objetivo, pero el efecto es insignificante. En el ejemplo, citado se aprecia claramente que características son útiles y cuáles no, pero en otros problemas puede no ser obvia la diferencia y requerir un mayor número de análisis de datos.
La reducción de dimensionalidad puede parecer que no tenga sentido, ya que cuando se presenten demasiadas funciones, también se necesitara un modelo más complejo, con más datos de entrenamiento y más potencia de cálculo para para entrenar al modelo de manera adecuada. Sin embargo, los modelos no comprenden la casualidad e intentan asignar cualquier característica incluida en su conjunto de datos a la variable objetivo, incluso si no existe una relación casual, generando modelos erróneos. Al reducir la cantidad de funciones se puede conseguir un modelo más simple y eficiente.
La reducción de dimensionalidad se encarga de identificar y eliminar las características que disminuyen el rendimiento del modelo de aprendizaje automático. Además, son varias las técnicas de dimensionalidad que se verán a continuación, y cada una de ellas es útil para determinadas situaciones.
¿Cómo reducir la dimensionalidad?
Entre los métodos más básicos de reducción de dimensionalidad, el más eficiente consiste en identificar y seleccionar un subconjunto de características que son muy relevantes para la variable objetivo. Esta técnica se conoce como la selección de funciones, siendo especialmente eficaz cuando se trata de datos tabulares en los que cada columna representa un tipo específico de información.
En la selección de características, principalmente, se realizan dos cosas: mantener las características que está altamente relacionadas con la variable objetivo y contribuir más a la variación del conjunto de datos. Por ejemplo, Python cuenta con una biblioteca, conocida como Scikit-learn, que cuenta con funciones para analizar y seleccionar funciones adecuadas para los modelos de Machine Learning.
Un aspecto común es emplear diagramas de dispersión y mapas de calor para visualizar la covarianza de diferentes características, es decir, se utilizan estas herramientas para conocer si dos características están altamente relacionadas entre sí y si tendrán un efecto similar en la variable de destino, para determinar que no es necesario incluir ambas en el modelo, eliminando una de ellas sin impactar negativamente en el rendimiento. Des mismo modo, se eliminan las variables que no aportan información a la variable objetivo.
Un ejemplo puede ser un conjunto de datos de 25 columnas que puede ser representado por únicamente 7 de ellas, capaces de representar el 95% del efecto sobre la variable objetivo. Así pues, se pueden eliminar hasta 18 funciones, simplificando el modelo de aprendizaje automático sin que este pierda eficiencia.
Generalmente, cuando se produce la reducción de dimensionalidades, se pierde hasta un 15% de la variabilidad en los datos originales, pero trae consigo ventajas como un menor tiempo de entrenamiento, requiere menos recursos computacionales y aumenta el rendimiento general de los algoritmos. Además, la reducción de dimensionalidad solventa el problema del sobreajuste. Cuando existen muchas características, los modelos se vuelven más complejos y tienden a sobreajustarse, gracias a la reducción este problema desaparece. A su vez, la reducción se encarga de la multicolinealidad, que ocurre cuando una variable independiente está altamente correlacionada con una o más variables independientes, así que la reducción combina esas variables en un único conjunto.
Por otro lado, esta técnica es muy útil también para el análisis factorial, enfoque que se encarga de localizar variables latentes que no se miden directamente en una sola variable, sino que infieres de otras variables en el conjunto de datos, donde las variables latentes se conoces como factores. Asimismo, se elimina el ruido en los datos al mantener únicamente las características más importantes y eliminando las redundantes, mejorando así la precisión del modelo.
En el ámbito de las imágenes es muy útil para su compresión, lo que permite minimizar el tamaño en bytes mientras se mantiene gran parte de la calidad de la imagen. Básicamente, los píxeles que forman una imagen se consideran variables de los datos de la imagen. Mediante un análisis de componentes principales (PCA) se mantiene un numero óptimo de componentes para equilibrar la variabilidad y la calidad de imagen.
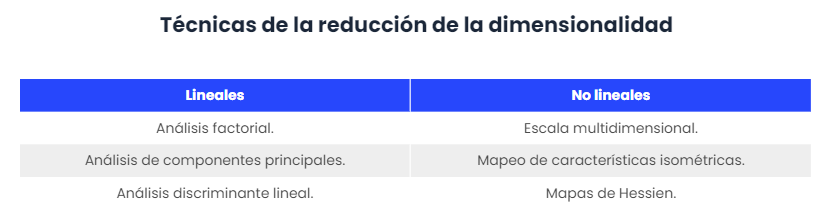
Por último, estas técnicas se diferencian entre lineales y no lineales, algunas de las más destacadas son:
Beneficios y desventajas de las técnicas de reducción de dimensionalidad
Algunos de los principales beneficios que genera aplicar la técnica de reducción de dimensionalidad son los siguientes:
- Reducir las dimensiones de las características implica una reducción del espacio requerido para almacenar el conjunto de datos, porque este también se reduce.
- El tiempo de entrenamiento de modelos es menor para dimensiones reducidas.
- Se facilita la visualización de datos más rápidamente gracias a la reducción de características del conjunto de datos.
- Desaparecen las características redundantes en el ámbito de la multicolinealidad.
La reducción de dimensionalidad también presenta ciertos inconveniente que se mencionan a continuación, aunque las ventajas son mayores:
- Se pueden perder algunos datos debido a la reducción de la dimensionalidad.
- En la técnica de reducción de dimensionalidad de PCA, en ocasiones no se conocen los componentes principales que se deben considerar.
Conclusiones
En resumen, tener demasiadas funciones provocará un modelo de Machine Learning ineficiente. Sin embargo, la capacidad de reducir características mediante la reducción de dimensionalidad es una herramienta que se puede emplear para crear modelos más optimizados y eficientes.
La reducción de dimensionalidad se puede aplicar a diferentes campos como, por ejemplo, los datos de alta dimensión, el reconocimiento de voz, visualización de datos, reducción de ruido o el procesamiento de señales, entre otros. También, se puede utilizar para transformar datos no lineales en una forma linealmente separable.
El uso de esta técnica trae consigo importantes beneficios que van desde la reducción del espacio de almacenamiento del conjunto de datos hasta la eliminación de características redundantes, pasando por una optimización del tiempo de entrenamiento de modelos y facilidad en la visualización de los datos. No obstante, es una técnica que requiere conocimiento y un equipo adecuado para realizarse, pues pueden eliminarse más datos de los debidos y generar un modelo erróneo.


